numpy.polynomial.chebyshev.chebval

numpy.polynomial.chebyshev.chebval(x, c, tensor=True)[source]

Evaluate a Chebyshev series at points x.

If c is of length n + 1, this function returns the value: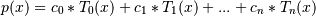

The parameter x is converted to an array only if it is a tuple or a list, otherwise it is treated as a scalar. In either case, either x or its elements must support multiplication and addition both with themselves and with the elements of c.

If c is a 1-D array, then p(x) will have the same shape as x. If c is multidimensional, then the shape of the result depends on the value of tensor. If tensor is true the shape will be c.shape[1:] + x.shape. If tensor is false the shape will be c.shape[1:]. Note that scalars have shape (,).

Trailing zeros in the coefficients will be used in the evaluation, so they should be avoided if efficiency is a concern.

Parameters:

x : array_like, compatible object If x is a list or tuple, it is converted to an ndarray, otherwise it is left unchanged and treated as a scalar. In either case, x or its elements must support addition and multiplication with with themselves and with the elements of c. c : array_like Array of coefficients ordered so that the coefficients for terms of degree n are contained in c[n]. If c is multidimensional the remaining indices enumerate multiple polynomials. In the two dimensional case the coefficients may be thought of as stored in the columns of c. tensor : boolean, optional If True, the shape of the coefficient array is extended with ones on the right, one for each dimension of x. Scalars have dimension 0 for this action. The result is that every column of coefficients in c is evaluated for every element of x. If False, x is broadcast over the columns of c for the evaluation. This keyword is useful when c is multidimensional. The default value is True. New in version 1.7.0.

Returns:

values : ndarray, algebra_like The shape of the return value is described above.

See also

chebval2d, chebgrid2d, chebval3d, chebgrid3d

Notes

The evaluation uses Clenshaw recursion, aka synthetic division.